PRML ベイズ線形回帰-オンライン学習版をJavaで書いてみる

作者: C. M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
出版社/メーカー: シュプリンガー・ジャパン株式会社
発売日: 2007/12/10
メディア: 単行本
購入: 18人クリック: 1,588回
この商品を含むブログ (110件) を見る

前回に続いて、今度は、第３章ベイズ線形回帰を書いてみる。

ベイズ的にといていくと、正則化と同じ項が出てくるのね。
やっぱり、逐次学習（オンライン学習）できるのも面白いよね。

ということで、オンライン学習版です。

グラフ描画XYGraphは、前回と同じものを利用しています。

見てもらうと、クラス内に訓練データを保持していないことがわかります。
wの平均mと分散Sのみを保持し、これを逐次的に更新していくことで、最終結果が得られます。

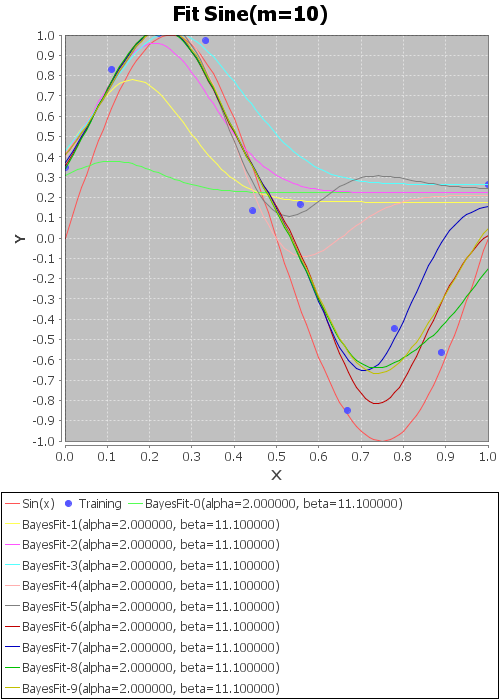
モデル数：10、基底関数：ガウス、alpha=2.0、beta=11.1
で、10点を入力に実行したのが以下。
かなり判りにくいけど、
赤い線→本物の線 sin(x)
青い点→訓練データ10点
そのほか→訓練データを追加したときのｗの結果（平均m）を用いて書いたyの曲線

この例では、訓練データはxが小さいほうから順番に入れているので、xが増えるにしたがって徐々にフィッティングしていくのがわかる。
さすがオンライン。

やってみるとわかるが、alphaとbetaを変えると、すごく結果が変わる。
かなりセンシティブ。
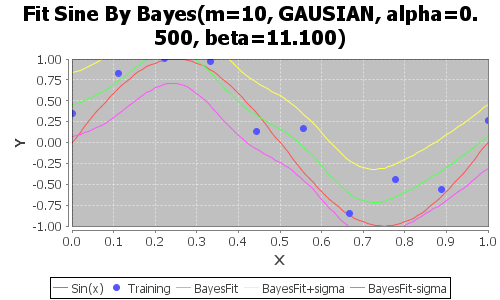
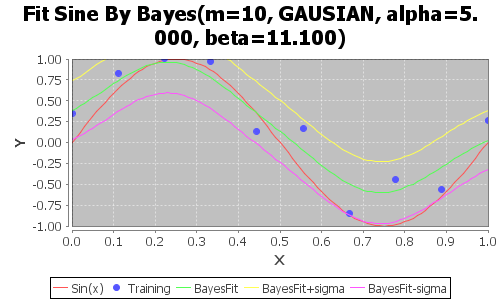
以下、betaを11.1に固定して、alphaだけ変えて、最終結果だけプロットしたものを示す。
ちなみに、訓練データの分散が0.3なので、beta=1/σ^2=11.1は真の値。

alhpa=0.05
黄色とピンクはw+σとw-σ見たいなイメージ。
黄色→wの平均mに分散Sを足したものをwとしてyをプロット
ピンク→wの平均mに分散Sを引いたものをwとしてyをプロット

alpha=0.5

alpha=5.0

alpha=50.0

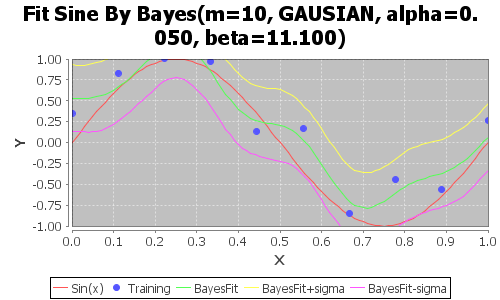
徐々になだらかになっていく。
しかし、あまりなだらかにしすぎると、sine(x)ともだいぶ離れてしまう。
実際に決めるのはなかなか難しい。

ということで、次回はエビデンスとalphaとbetaの最適化を試してみようと思う。

では。

package prml.chap3;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.ArrayList;
import java.util.List;

import prml.util.XYGraph;

import Jama.Matrix;

/**
 * 線形回帰モデル：ベイズ-オンライン学習（基底関数を選択）
 */
public class LinearRegressionByBayesOnline {
	int numM;
	BasisFunction func;
	double alpha;
	double beta;
	Matrix mN;
	Matrix SNInv;

	public LinearRegressionByBayesOnline(int numM, BasisFunction func, double alpha,
			double beta) {
		this.numM = numM;
		this.func = func;
		this.alpha = alpha;
		this.beta = beta;
		this.mN = new Matrix(numM, 1);
		this.SNInv = new Matrix(numM, numM);

		// 事前分布
		// m_0 は全部0
		for (int i = 0; i < numM; i++) {
			mN.set(i, 0, 0.0);
		}

		// S_0^-1 = α * I
		Matrix I = new Matrix(numM, numM);
		for (int i = 0; i < numM; i++) {
			for (int j = 0; j < numM; j++) {
				if (i == j)
					I.set(i, j, 1.0);
				else
					I.set(i, j, 0.0);
			}
		}
		SNInv = I.times(alpha);
	}

	// パラメータmを取得
	public double[] getParamM() {
		return mN.getColumnPackedCopy();
	}

	// パラメータSを取得
	public double[][] getParamS() {
		return SNInv.inverse().getArrayCopy();
	}

	// 逐次学習
	public void learnOnline(double x, double t) {
		// 学習データ:(x,t)={(x_1,t_1),...,(x_n,t_n)
		// 曲線フィット：y(x,w) = w_0 * φ_0(x) + w_1 * φ_1(x) + w_2 * φ_2(x) ...
		//                  = ��_j={0〜M-1} w_j * φ_j(x)

		// w事後分布逐次学習：
		// p(w|t)=ガウス(w|m_N, S_N)
		// m_N+1 = S_N+1 ( S_N^-1 * m_N + β * Φ_N+1 * t_N+1 )
		// S_N+1^-1 = S_N^-1 + β * Φ_N+1 * Φ_N+1^T )
		// (m:M次元(wのガウス分布平均), S:M*M次元(ガウス分布の分散))
		// (Φ_N:M*1次元, t_N:スカラー)
		// Φ_N+1{j} = φ_j (x_N+1)

		// 計画行列 Φ の学習対象データのみ Φ_N+1
		Matrix PHIN1 = new Matrix(this.numM, 1);
		for (int j = 0; j < numM; j++) {
			double val_PNj = func.phi(j, x);
			PHIN1.set(j, 0, val_PNj);
		}

		// 事後分布を更新
		Matrix SN1Inv = this.SNInv.plus(PHIN1.times(PHIN1.transpose()).times(this.beta));
		Matrix mN1 = SN1Inv.inverse().times(
				this.SNInv.times(this.mN).plus(
						PHIN1.times(t).times(this.beta)));

		this.SNInv = SN1Inv;
		this.mN = mN1;
	}

	public static void main(String args[]) throws IOException {
		// 学習データファイル名
		String filename = args[0];
		// モデルのパラメータ数
		int m = Integer.parseInt(args[1]);
		// 基底関数
		String BasisFuncName = args[2];
		// alpha, beta
		double alpha = Double.parseDouble(args[3]);
		double beta = Double.parseDouble(args[4]);

		// 基底関数選択
		BasisFunction func = null;
		if (BasisFuncName.equals("GAUSIAN")) {
			func = new GausianBasisFunction(m, 0.0, 1.0);
		} else if (BasisFuncName.equals("POLY")) {
			func = new PolynomialBasisFunction();
		}

		// フィッティングオブジェクト
		LinearRegressionByBayesOnline lrBayesOnLine = new LinearRegressionByBayesOnline(m, func,
				alpha, beta);

		// データをロードして学習データとして追加しながら学習
		BufferedReader br = new BufferedReader(new FileReader(
				new File(filename)));
		String line;
		List<double[]> trainData = new ArrayList<double[]>(); // グラフ描画用にデータを保持
		List<double[]> w_Avgs = new ArrayList<double[]>(); //各学習結果の重みwを保持
		try {
			while ((line = br.readLine()) != null) {
				String recStr[] = line.split(" ", 2);
				double[] rec = { Double.parseDouble(recStr[0]),
						Double.parseDouble(recStr[1]) };
				trainData.add(rec);
				lrBayesOnLine.learnOnline(rec[0], rec[1]); //学習
				w_Avgs.add(lrBayesOnLine.getParamM()); //wの事後分布の平均
			}
			br.close();
		} catch (IOException e) {
			e.printStackTrace();
		}

		// グラフ描画用
		// 正解データ
		double[][] sineValues = makeSineValues();
		// 訓練データ
		double[][] trainValues = makeTrainValues(trainData);
		// 学習結果
		List<double[][]> resultValues = new ArrayList<double[][]>();
		for(int i=0; i<w_Avgs.size(); i++){
			resultValues.add(makeResultValues(w_Avgs.get(i), m, func));
		}
		// グラフ表示
		XYGraph xyGraph = new XYGraph("Fit Sine(m=" + String.valueOf(m) + ")",
				"X", "Y");
		xyGraph.addDataValues("Sin(x)", sineValues, true);
		xyGraph.addDataValues("Training", trainValues, false);
		for(int i=0; i<resultValues.size(); i++){
			xyGraph.addDataValues(
					String.format("BayesFit-%d(alpha=%f, beta=%f)", i, alpha, beta),
					resultValues.get(i), true);
		}
		xyGraph.rangeX(0.0, 1.0);
		xyGraph.rangeY(-1.0, 1.0);
		xyGraph.saveGraphAsPNG("sin-bayes-online.png", 500, 300); // viewメソッドの後に呼び出すと、動作がおかしいので注意
		xyGraph.view(700, 700);
	}

	private static double[][] makeSineValues() {
		double[][] ret = new double[2][101];
		// 0-1を100個のデータで埋める
		for (int i = 0; i <= 100; i++) {
			ret[0][i] = i / 100.0; // X
			ret[1][i] = Math.sin(2.0 * Math.PI * ret[0][i]); // Y
		}
		return ret;
	}

	private static double[][] makeTrainValues(List<double[]> trainingDataValues) {
		double[][] ret = new double[2][trainingDataValues.size()];
		int i = 0;
		for (double[] rec : trainingDataValues) {
			ret[0][i] = rec[0]; // X
			ret[1][i] = rec[1]; // Y
			i++;
		}
		return ret;
	}

	private static double[][] makeResultValues(double[] w, int m,
			BasisFunction func) {
		double[][] ret = new double[2][101];
		// 0-1を100個のデータで埋める
		for (int i = 0; i <= 100; i++) {
			ret[0][i] = i / 100.0; // X
			for (int j = 0; j < m; j++) { // Y
				ret[1][i] += w[j] * func.phi(j, ret[0][i]);
			}
		}
		return ret;
	}
}

基底関数のインターフェースクラス

package prml.chap3;

/**
 * 線形回帰の既定関数用インターフェース
 */
public interface BasisFunction {
	public double phi(int i, double x);
}

ガウス基底関数クラス

package prml.chap3;

/**
 * ガウス基底関数
 */
public class GausianBasisFunction implements BasisFunction {

	double[] u;
	double s;

	// パラメータを指定する
	// ガウスの平均と分散を指定。
	// ただし、u[0]は無視する。（u[0]はφ_0(x)に相当し、このときは必ずφ_0(x)=1であるため）
	public GausianBasisFunction(double[] u, double s) {
		this.u = u;
		this.s = s;
	}

	// 定義域とモデル数を指定。パラメータは自動決定
	public GausianBasisFunction(int m, double begin, double end) {
		this.u = makeAutoParamU(m, begin, end);
		this.s = makeAutoParamS(m, begin, end);;
	}

	// 基底関数の結果
	// ただし、j=0の場合、必ず１を返す。
	@Override
	public double phi(int j, double x) {
		if (j == 0) {
			return 1;
		}
		return Math.exp(-1 * Math.pow(x - u[j], 2) / (2 * s * s));
	}

	// パラメータuを自動的に調整する
	// 定義域を、M個で等分に分割する位置にする。
	// 戻り値： ret[1...m] = param u[1...m]
	// ex:M=10, 定義域：0.0 - 1.0
	// u = NaN, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9
	private static double[] makeAutoParamU(int m, double begin, double end) {
		double[] u = new double[m];
		
		double s = (end - begin) / m;
		u[0] = Double.NaN; //ret[0]は使わない
		for (int i = 1; i < m; i++) {
			u[i] = begin + s * i;
		}
		return u;
	}

	// パラメータsを自動的に調整する（定義域をモデル数で等分割）
	// 戻り値：param s
	// ex:m=10, 定義域：0.0 - 1.0
	// s = 0.1
	private static double makeAutoParamS(int m, double begin, double end) {
		double s = (end - begin) / m;
		return s;
	}
}

多項式基底関数クラス

package prml.chap3;

/**
 * 多項式基底関数
 */
public class PolynomialBasisFunction implements BasisFunction {

	@Override
	public double phi(int j, double x) {
		if (j == 0) {
			return 1;
		}
		return Math.pow(x, j);
	}

}